NCERT Solutions for Class 9 Maths Ex 1.3

 

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3

Ex 1.3 Class 9 Maths Question 1.

Write the following in decimal form and say what kind of decimal expansion each has

Solution:
(i) We have, 36100 = 0.36
Thus, the decimal expansion of 36100 is terminating.

(ii) Dividing 1 by 11, we have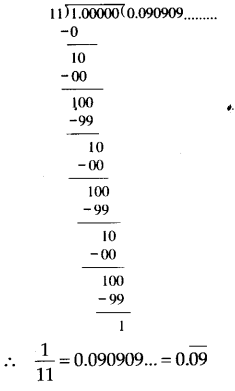

Thus, the decimal expansion of 111 is non-terminating repeating.

(iii) We have, 418 = 338
Dividing 33 by 8, we get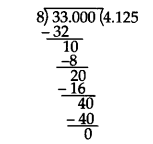

∴ 418 = 4.125. Thus, the decimal expansion of 418 is terminating.

(iv) Dividing 3 by 13, we get

Here, the repeating block of digits is 230769
∴ 313 = 0.23076923… = 0.230769¯
Thus, the decimal expansion of 313 is non-terminating repeating.

(v) Dividing 2 by 11, we get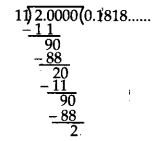

Here, the repeating block of digits is 18.
∴ 211 = 0.1818… = 0.18¯
Thus, the decimal expansion of 211 is non-terminating repeating.

(vi) Dividing 329 by 400, we get

∴ 329400 = 0.8225. Thus, the decimal expansion of 329400 is terminating.

Ex 1.3 Class 9 Maths Question 2.

You know that 17 = 0.142857¯. Can you predict what the decimal expansions of 27 , 137 , 47 , 57 , 67 are , without actually doing the long division? If so, how?
Solution:
We are given that 17 = 0.142857¯.
∴ 27 = 2 x 17 = 2 x (0.142857¯) =0.285714¯
37 = 3 x 17 = 3 x (0.142857¯) = 0.428571¯
47 = 4 x 17 = 4 x (0.142857¯) = 0.571428¯
57 = 5 x 17 = 5 x(0.142857¯) = 0.714285¯
67 = 6 x 17 = 6 x (0.142857¯) = 0.857142¯
Thus, without actually doing the long division we can predict the decimal expansions of the given rational numbers.

Ex 1.3 Class 9 Maths Question 3.

Express the following in the form pq where p and q are integers and q ≠ 0.
(i) 0.6¯
(ii) 0.47¯
(iii) 0.001¯¯¯¯¯¯¯¯
Solution:
(i) Let x = 0.6¯ = 0.6666… … (1)
As there is only one repeating digit,
multiplying (1) by 10 on both sides, we get
10x = 6.6666… … (2)
Subtracting (1) from (2), we get
10x – x = 6.6666… -0.6666…
⇒ 9x = 6 ⇒ x = 69 = 23
Thus, 0.6¯ = 23

(ii) Let x = 0.47¯ = 0.4777… … (1)
As there is only one repeating digit, multiplying (1) by lo on both sides, we get
10x = 4.777
Subtracting (1) from (2), we get
10x – x = 4.777…… – 0.4777…….
⇒ 9x = 4.3 ⇒ x = 4390
Thus, 0.47¯ = 4390

(iii) Let x = 0.001¯¯¯¯¯¯¯¯ = 0.001001… … (1)
As there are 3 repeating digits,
multiplying (1) by 1000 on both sides, we get
1000x = 1.001001 … (2)
Subtacting (1) from (2), we get
1000x – x = (1.001…) – (0.001…)
⇒ 999x = 1 ⇒ x = 1999
Thus, 0.001¯¯¯¯¯¯¯¯ = 1999

Ex 1.3 Class 9 Maths Question 4.
Express 0.99999… in the form pqAre you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Solution:
Let x = 0.99999….. …. (i)
As there is only one repeating digit,
multiplying (i) by 10 on both sides, we get
10x = 9.9999 … (ii)
Subtracting (i) from (ii), we get
10x – x = (99999 ) — (0.9999 )
⇒ 9x = 9 ⇒ x = 99 = 1
Thus, 0.9999 =1
As 0.9999… goes on forever, there is no such a big difference between 1 and 0.9999
Hence, both are equal.

Ex 1.3 Class 9 Maths Question 5.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 117? Perform the division to check your answer.
Solution:
In 117, In the divisor is 17.
Since, the number of entries in the repeating block of digits is less than the divisor, then the maximum number of digits in the repeating block is 16.
Dividing 1 by 17, we have

The remainder I is the same digit from which we started the division.
∴ 117 = 0.0588235294117647¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Thus, there are 16 digits in the repeating block in the decimal expansion of 117.
Hence, our answer is verified.

Ex 1.3 Class 9 Maths Question 6.
Look at several examples of rational numbers in the form pq (q ≠ 0). Where, p and q are integers with no common factors other that 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Solution:
Let us look decimal expansion of the following terminating rational numbers:


We observe that the prime factorisation of q (i.e. denominator) has only powers of 2 or powers of 5 or powers of both.

Ex 1.3 Class 9 Maths Question 7.
Write three numbers whose decimal expansions are non-terminating non-recurring.
Solution:
√2 = 1.414213562 ………..
√3 = 1.732050808 …….
√5 = 2.23606797 …….

Ex 1.3 Class 9 Maths Question 8.
Find three different irrational numbers between the rational numbers 57 and 911 .
Solution:
We have,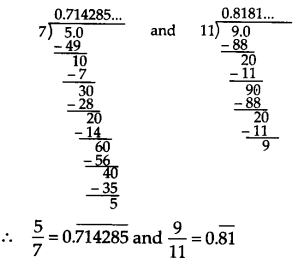

Three irrational numbers between 0.714285¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ and 0.81¯¯¯¯¯ are
(i) 0.750750075000 …..
(ii) 0.767076700767000 ……
(iii) 0.78080078008000 ……

Ex 1.3 Class 9 Maths Question 9.
Classify the following numbers as rational or irrational
(i) 23−−√
(ii) 225−−−√
(iii) 0.3796
(iv) 7.478478…..
(v) 1.101001000100001………
Solution:
(1) ∵ 23 is not a perfect square.
∴ 23−−√ is an irrational number.
(ii) ∵ 225 = 15 x 15 = 152
∴ 225 is a perfect square.
Thus, 225−−−√ is a rational number.
(iii) ∵ 0.3796 is a terminating decimal.
∴ It is a rational number.
(iv) 7.478478… = 7.478¯¯¯¯¯¯¯¯
Since, 7.478¯¯¯¯¯¯¯¯ is a non-terminating recurring (repeating) decimal.
∴ It is a rational number.
(v) Since, 1.101001000100001… is a non terminating, non-repeating decimal number.
∴ It is an irrational number.